쉽게 설명한 Minhash 알고리즘

• #minhash
• #hash
• #algorithm
• #locality-sensitive-hash
• #lsh

TL;DR

Minhash 는 Jaccard similarity 결과와 비슷한 분포를 가지게 차원을 축소해주는 알고리즘이다.

시작하며

예전에 이미지 추천한다고 LSH(locality sensitive hash) 를 사용했던 코드를 보다가 LSH 가 대체 어떻게 동작하는거지? 하는 의문이 생겼다.

거의 완벽하게 설명한 글¹이 있기 때문에 전체 내용을 다시 적지 않을 것이다.

여기서는 내 기준에 여러번 읽어도 이해가 잘 안됐던 내용들만 적어 본다.

또, 글에서도 언급한대로 실제로 구현을 했을 때는 이론 그대로 하면 퍼포먼스가 현저히 떨어진다. 가장 직관적인 구현체라고 생각되는 Datasketch² 를 기준으로 구현한 소스 코드를 간략히 설명해보겠다.

설명

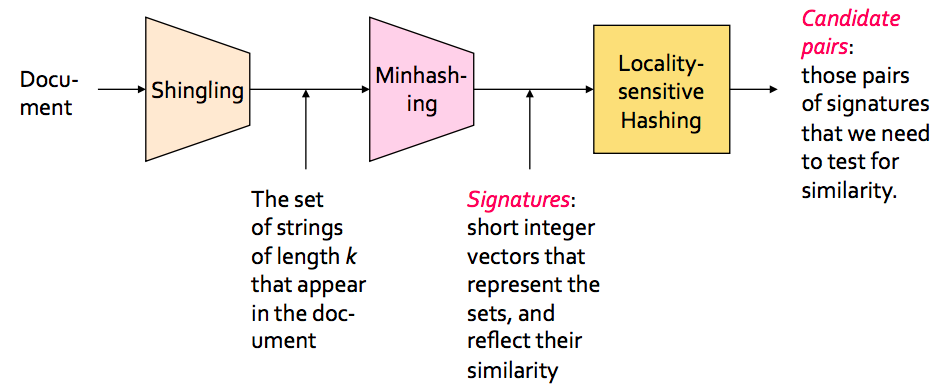
Shingling

자연어 처리 튜토리얼 같은걸 해봤다면 n-gram³ 을 들어봤을 것이다. 완전 동일한 개념이라고 보면 된다.

간단히 설명하면 I think Apex legends rocks! 라는 문장이 있을 때 아래와 같이 n 개로 묶은 그룹으로 재표현 해주는 것이다.

이렇게 하지 않으면 Apex legends rocks! I think Jaccard 유사도 계산시 이 문장은 위와 동일한 문장이라고 점수가 계산될 것이다.

# 2 gram
bigram = [
    'I_think',
    'think_Apex',
    'Apex_legends',
    'legends_rocks!',
]

# 3 gram
trigram = [
    'I_think_Apex',
    'think_Apex_legends',
    'Apex_legends_rocks',
]

방금 예에서는 편하게 보여주려고 공백을 기준으로 나누었지만 보통은 그냥 글자단위로 나누곤 한다.

# 3 gram
trigram = [
    'I_t',
    '_th',
    'thi',
    ...
    'ock',
    'cks',
    'ks!',
]

글에는 빠져있지만 보통 자연어 처리를 할 때 아래와 같은 전처리를 거친다.

1. 쓰레기 값을 날리고 (특수문자, 필요없는 prefix, postfix 등)
2. 형태소 분석기로 의미있는 단어만 남기고 (명사, 동사, 부사 등. 동사는 원형으로 변환해서 쓰기도 한다.)
3. 2-gram(bigram) 이나 3-gram(trigram) 를 적용

Minhash

Minhash 는 아래 3개의 스텝으로 구성되어 있다.

1. Shingle 들로 구성된 Matrix 를 만든다. 문서의 그림에서 Matrix 의 각 컬럼은 하나의 문서와 같다.
2. Matrix 의 row 인덱스 를 셔플한 리스트(permutation 이라고 부름)를 여러개 만든다.
3. 각 컬럼에 대해 permutation 을 1~n 까지 순서대로 확인하면서, 1이 나오면 Signature matrix 를 permutation 번호로 채운다.

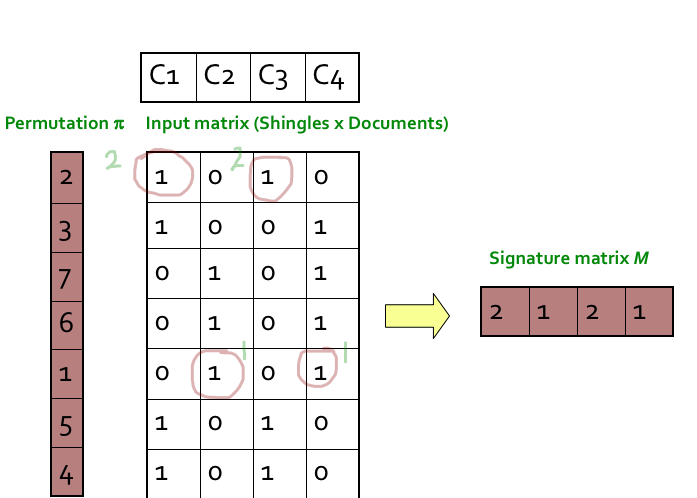
3번이 원문의 내용과 그림만 봐서는 이해가 안될 수 있어서, 좀 더 상세히 적어본다. 첫 Signature matrix 가 2, 1, 2, 1 인데, 이것은 아래 순서를 통해 만들어진다.

1. 최종 생성해야하는 Signature matrix 의 값은 permutation index 이다.
2. permutation 을 순서대로 선택하고 (1~7 순서)
3. permutation 에 해당하는 Matrix 의 컬럼값이 1 이면 동일한 컬럼에 해당하는 signature matrix 를 permutation index 로 채운다.
4. permutation index 가 작은 순서대로 row 를 선택하여 진행한다.
5. 순열의 가장 작은값 1은 Matrix 의 5번째 row를 가리키고 있다.
6. Matrix 의 5번째 row 는 C2, C4 가 1 이므로 signature matrix 의 2, 4 번째에 permutation index 인 1 을 채워준다.
7. 두번째로 작은 값은 2 이고, 해당하는 Matrix 의 2번째 row 의 C1, C3 이 1 이다. 따라서 signature matrix 의 1, 3 번째에 permutation index 인 2 를 채워서 permutation 하나의 signature 를 만들어냈다.

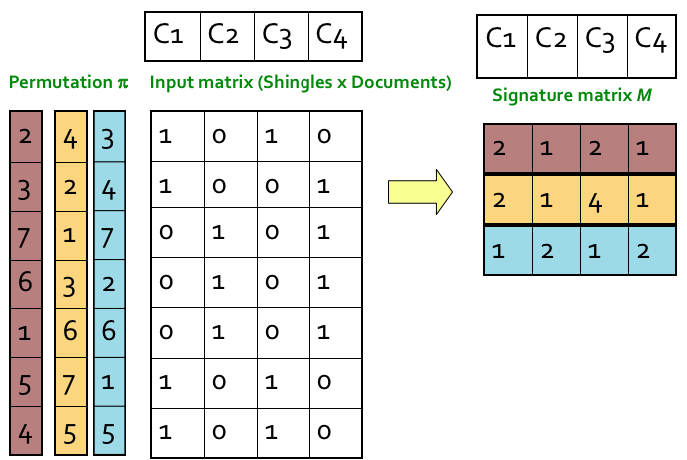
3개의 permutation 을 쓰면 위 그림처럼 7바이트의 데이터를 3바이트로 표현할 수 있다.

보통 input 은 문서이고 shingling 을 거치면 엄청 큰 크기의 배열이 된다. 대부분의 경우 대략 128 정도의 길이(128 개의 permutations)로 signature matrix 를 만들면 적절한 결과를 얻을 수 있다.

구현

컨셉

글만 보고 실제로 구현해보면 아래 2개의 문제점을 만나게 된다.

1. permutation 을 랜덤하게 계속 만들어줘야 한다. 1번에 비하면 크지 않은 계산량이지만 여튼 랜덤을 동적으로 계속 부르는 것은 부담이 된다.
2. Shingling Matrix 를 만들어야 한다. 즉, 모든 shingle 에 대한 목록을 가지고 있어야 0, 1 로 세팅할 수 있다. 이러면 새로운 문서가 추가 될 때 마다 모든 signature 를 다시 계산해줘야 한다.

minhash 구현체를 몇개 뜯어 봤는데 datasketch 의 구현체가 가장 직관적이고 깔끔한 코드를 가지고 있는 것 같아서 이걸 기반으로 설명하겠다.

datasketch 는 위의 문제점을 아래방법으로 해결했다.

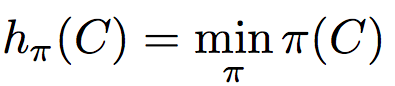
1. psuedo random generator 를 통해 미리 permutations 를 만들어둔다. 즉, seed 가 동일한 Minhash 는 동일한 permutations 를 가진다.
2. permtations 크기와 동일한 signature 매트릭스를 미리 만들어두고, shingle 이 추가되면 모든 permutations 에 대해 유니버설 해싱으로 해시를 해주고, 가장 작은 값들로 signature 매트릭스를 업데이트 해준다.

직관적으로 유니버설 해싱을 사용하는 이유를 설명하지는 않았지만, shingle 간 충돌을 줄이고, signature 매트릭스의 값이 고루 분포되도록 하는 목적으로 생각된다.

코드 설명

코드는 여기⁴

TODO: 디테일한 설명추가하자...
메르센 소수, binascii.crc32

마치며

minhash 사용된 테크닉 만으로도 여기저기 소소하게 적용해볼 여지가 있어서 재미있었다.

다음은 참고글의 후반부인 LSH(Locaility Sensitive Hash) 를 설명하고 구현하는 부분을 마저 적어볼 예정이다.